A Tutorial on Phase Space, Attractors and the Adams Conjecture
One of the delights of reading Levi Bryant is finding familiar terms in unfamiliar contexts. I’m thinking of such terms as phase space and attractor. I know them as mathematical terms but Bryant uses them in contexts where the mathematics is irrelevant, though apparently intended. In the manner of the grand masters of old, and of the seers and wizards of the inscrutable Orient, he uses them as provocations to prod us along our own journeys.
I have an imp of perversity in me. I intentionally choose words that I know will provoke. That provocation is not just a provocation towards whatever readers I might happen to have, but towards myself as well. How can I manage to think? How can I engender thought in myself? It doesn’t come naturally or automatically.
It is thus indeed a wonder that Sensei manages to think at all, making it triply gracious of him to pass on his hard won wisdom to us.
It is in this spirit of elucidatory nonsense that I offer the following thoughts about Bryant’s blue mug, a philosophic talisman he has used to develop some basic concepts. First I offer two passages from the Master himself, passages about his beloved blue mug. In the next two sections I argue that those passages are unintelligible if one understands phase spaces and attractors as physicists do. I then contrast Bryant’s scientistic use of jargon with Lévi-Strauss’s superficially similar, but deeply different, rhetoric of algebra. I conclude with a set of exercises for the reader interested in further explorations of jargon space.
The Blue Mug
Here is a passage from Bryant’s post of 30 April 2010, The Mug Blues:
When I distinguish between the virtual proper being of an object and the actual local manifestation of an object, I am attempting to distinguish between the object qua substance or enduring unity and the object qua qualities or properties. The virtual proper being of an object is its substantiality, its being as substance, or its being as a (more or less) enduring unity. It is what makes the object properly an object. No one or thing ever encounters an object qua substance for the substance of an object is perpetually withdrawn or in excess of any of its manifestations. Rather, the proper being of an object can only ever be inferred from its local manifestations in the world. By contrast, the local manifestation of an object is the manner in which a substance or virtual proper being is actualized in the world under determinate conditions.
That much I understand, I think, and it establishes Bryant’s own terms of art, virtual proper being and local manifestation.
Master Levi’s provocations begin in when he introduces terms I’m familiar with from reading nonlinear dynamics and chaos theory and discussing them with others, such as Tim Perper, whom I mentioned in my post about entropy, and Walter Freeman, a neuroscientist at Berkeley. Consider this passage from Bryant’s post of 5 May 2010, Regimes of Attraction:
Were we to plot a two-dimensional graph on an x-y axis, the entire range of points on that graph would denote the coloring power of the mug, while the radiant blue of the mug in bright sunlight would be a point on this graph, not the entire line of the graph. Accordingly I distinguish between attractors, phase spaces, and qualities. Attractors, within the framework of onticology, are powers that refer to an entire range of qualities an object can actualize. Phase spaces refer to all possible points (usually infinite) that can be occupied within the space of that attractor. And qualities refer to points actualized within that phase space such as a specific shade of blue. The photograph at the beginning of this post is a particularly nice illustration of this as we see that the mug is two shades of blue, thereby actualizing two different points in the phase space of its attractor or power at once. We here encounter the rationale behind the terminological choice to refer to qualities as “local manifestations”. First, these are manifestations in the sense that they are events or occurrences that take place within an object. Qualities are things that happen, not something that an object has.
I note first that that last sentence seems quite important to Bryant. I find it a little strange to think of the mug’s blueness as something it does rather than as something it has, but only a little. But, burdened as I am by prior acquaintance with attractors and phase spaces, Bryant’s use of those terms seems, shall we say, somewhat exotic and mysterious, perhaps even—dare I say it?—flat out nonsense.
Pseudo Phase Spaces
While color theorists DO talk of color space, many of them in fact, and the web is littered with sites discussing color spaces (the post popular ones seem intended primarily to support digital photographers), they do not, in my experience, talk of phase spaces. The notion of phase space is typically used to discuss mechanical systems, but the concept certainly has other application domains, e.g. neuroscientists use it to characterize brain activity. As the Wikipedia entry indicates ”a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space.”
THAT seems to be the notion that Bryant wants. He wants to think of an object’s virtual proper being as a space, say, VPB space, in which each point represents one state of the object. At any given moment in time the object will be in one of those states; that’s a local manifestation. It is by no means obvious, however, that every point in VPB space will be actualized. VPB space is infinite while the life span of any given object is finite. Some of those points, that is to say, states, are not likely to be occupied.
Though, come to think of it, if the universe operated according to Nietzsche’s principle of eternal recurrence, or according to various notions of reincarnation, it might possible for a being to traverse its entire VPB space in the course of many life times each of finite extent. One might conjecture that the entire universe corresponds to the real numbers while each VPB space corresponds only to the integers. In that way this supposition might be wrangled into acceptable form. To do that we’d have to...
I digress.
The problem with Bryant’s usage is that he doesn’t give us an explicit construction. He simply asserts his phase space into existence. Why two dimensions? Why not one, or three, or 17, or leventy-leven? And it’s not clear whether he’s asserting a phase space for the mug or only for the mug’s color. Without some clarification of these matters we cannot begin to make sense of his talk of phase space.
What’s worse, Bryant isn’t particularly interested in mugs and blueness. He’s interested in all objects and all their qualities. The mug, with its blueness, is simply one example. If he wants to apply the concept of phase space to ALL objects, which for him includes various collections and groups and processes, then the concept of phase space must be developed for each class of objects.
In so far as kumquats, planets, bacteria, bushes, and ponds are physical objects having shape, mass, odor, taste, texture, and color, the same construction might suffice for them—I say “might” because I’m just making this up as I go. I’ve not attempted to think these things through. But it is by no means obvious that those parameters exhaust these objects. Some or all those classes of objects may well require other parameters for their representation, and thus other phase spaces.
What about zoos, roving bands of Ethiopian pirates, local area computer networks, municipal water authorities, and Mogul miniatures, all of which are objects in Bryant’s philosophical sense? How does one construct phase spaces appropriate for them? Without explicit and detailed construction the notion of a phase space for such things can be little more than a pile of exotic verbiage.
Phase Space and Attractors
So, how do physicists use the notion of phase space concept to characterize the behavior of a volume of gas or a liquid? In this case we have a dimension of space for each molecule. Well, actually we have six dimensions for each molecule; three of those dimensions carry information about spatial position and, as gas molecules move, three characterize a molecule’s momentum. If a volume of gas contains only three molecules, then the phase space will contain 18 dimensions, way more than we can visualize.
But physicists generally are not interested in volumes of gas containing only three molecules. The volumes they’re interested in contain, in the phrase of Carl Sagan, billions and billions of molecules. That requires a space of very high dimensionality indeed.
Such a space treats each individual molecule as an autonomous object—something which should be attractive to Bryant and to fellow object-oriented ontologists. But it makes for messy math. It is, however, possible to do a great deal of interesting and important physics using only two dimensions, temperature and pressure. That is to say, it is possible to project behavior in high-dimensional spaces into spaces of low dimensionality. The two-dimensional projection onto temperature and pressure is said to characterize the macrostates of the system while the full high-dimensional phases space is necessary to characterize its microstates.
Consider the system I photographed in Entropy and Self-Organization on the Table Top. In a sense it is a very simple system, consisting of a tumbler filled with ordinary tap water into which we introduce two or three drops of black ink. But the physics of that system is in fact quite complex and needs to be studied at the micro level, where each molecule is considered to be a quasi-autonomous actor. Thus each molecule is assigned six dimensions (3 position, 3 momentum) in the phase space.
Consider this photo, the first one I took:
Let’s do a crude calculation. The system has three spatial dimensions which the photograph flattens (projects) into two. The original of this photo measures 2670 by 2003 pixels making a total of 5,348,010 pixels. Think of that as a two-dimensional measurement of the evolving system taken at an “instant” of time. That measurement space alone would then require 5,348,010 dimensions. It contains no momentum information at all and each individual pixel is, in effect, a “smear” of billions upon billions of molecules.
So it’s a pretty poor proxy for real measurement. But it’s enough to give some intuitive sense of complexity and strangeness of these conceptual objects, these phase spaces. In phase space, moreover, that state is represented by a single point. A single point.
Here’s the fourth photo I took:
That state too, however rich and complex it appears in the photographic measurement, is only one point in the phase space. Likewise, the final state is but a point in the phase space (ignore the light vertical streaks on the glass; they're reflections; the dark vertical ellipse at top center is the camera lens):
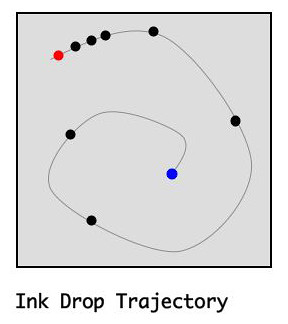
The sequence of states a system occupies during its evolution is called its trajectory. That trajectory can be visualized by projecting it into a 3D or 2D space. In the next image I show what such a projection might look like for this system:
Note that I do not in fact know what that trajectory would look like in 2D projection. I made this image purely for illustrative purposes. The nine points represent the nine photographs I took. Each represents a single micro state of the system, all zillions of dimensions. The red point is the first photograph while the blue point is the last. The light gray line represents a WAG (wild-ass guess) about the whole trajectory. Whether or not it’s correct is irrelevant. What’s important is that there IS a trajectory.
If you were to perform this little demonstration many times, it would become evident that, no matter where the ink was dropped into the tumbler, the final state would always be the same. The different trajectories might be somewhat different in character, but the final point is always the same. That final point is called the system’s attractor.
The name is unfortunate as it suggests that there is something THERE that is ATTRACTING the system to that state, like bees to honey or iron files to a magnet. There isn’t. Nothing is attracting in that way; there’s nothing attractive about that point. It’s just that, given the internal dynamics of the system, that’s how things work out.
A metaphor that’s commonly used is that of releasing a small ball into a basin from the basin’s edge. No matter where you place the ball on the edge of the basin it will always roll down the side to the center. The center is the attractor and the basin itself is an attractor basin.
Now let us consider a passage from Guru Levi. This is from the blue mug text quoted above:
Attractors, within the framework of onticology, are powers that refer to an entire range of qualities an object can actualize. Phase spaces refer to all possible points (usually infinite) that can be occupied within the space of that attractor.
The onticological attractor is a power or powers; the dynamical attractor is not. The onticological phase space is "within the space of [an] attractor"; the dynamical phase space has an attractor within it. As far as I can tell, the onticological attractor is but a distant echo of the dynamical attractor. The spelling’s the same but the concepts are not.
Lévi-Strauss’s Rhetoric of Algebra
By way of contrast I’d like to consider the pseudo-algebra that Lévi-Strauss used in Mythologies, his four-volume study of myth. Here is what he says early in The Raw and the Cooked, the first of the four volumes. Of his “occasional use of logico-mathematical symbols” (p. 30):
There is only a superficial resemblance between my formulas and the equations of the mathematicians, because the former are not applications of rigorously employed algorisms, allowing the demonstration of various points to be interlinked or condensed.
At this point Bryant may well claim that his usage is no different. However, he makes no such explicit disavowal as does Lévi-Strauss and there are passages in his blog and in his book where he explicitly discusses the science without making any explicit and firm distinction between the science and his philosophical system.
For example, in a post from 10 October 2011, More on Vitalism, Bryant has a YouTube video of a chemical reaction that oscillates between appearing blue and appearing red without ever settling on one state or the other. The reaction is a classic one in the study of nonlinear dynamics. But when Bryant uses terms that chemists use to describe such reactions – e.g. phase space, attractor, trajectory – he leaves the signifieds behind and retains only the signifiers, supplying his own signifieds. Thus the chemistry cannot and does not provide any support or authority for Bryant’s own theorizing. And yet that is what he wants from such references, support and authority.
He can’t have it both ways. If he wants the support and authority, then he must use the correct concepts. If he wants free conceptual reign, then he should stop invoking the science itself and admit that it provides no support for his ideas. Whatever Bryant is doing in such passages, which are numerous, he is not, as he often claims, incorporating scientific thinking about complexity and nonlinear dynamics into his philosophical system.
Let’s continue with Lévi-Strauss (pp. 30-31):
The formulas that I have written with the help of symbols borrowed from mathematics ... are not intended to prove anything; they are meant rather to suggest in advance the patterns of some discursive account, or to sum up such an account, by bringing within a single purview complex groups of relations and transformations, the detailed description of which may have sorely tried the reader’s patience. Far from replacing such a description, their function is merely to illustrate it in a simplified form...
As I have argued in my post, Harman, Wittgenstein, Math&Logic, Compositionism, Biology, Lévi-Strauss’s use of such terms is fundamentally rhetorical. He quotes and summarizes the myth texts at some length and the comparisons he makes between them, two, three, four, and more at a time, are complex. His formulae and diagrams call our attention to these complex comparisons and make them more comprehensible. He is calling our attention to the world, not distracting us from it.
Bryant’s usage is quite different. His blog posts and his book, The Democracy of Objects, are filled with many examples from many domains. All are offered quickly and lightly, with little detail. All depend on their matrix domain for their intelligibility and coherence. Bryant’s terminology adds nothing to them. Rather, it serves like the hooks that allow one to hang ornaments on a tree. Bryant’s philosophical system is the tree and he treats the world as a source of ornaments for decorating it.
* * * * *
Addendum, 7 July 2012: Bryant has just posted on Onto-Cartography, his current project:
I’m pitching onto-cartography as a new sort of critical theory that explores the way in which space-time paths emerge from interactions among entities as well as signifying components. The idea is that entities and signs exercise what I call “gravity”, creating vectors or paths along which other entities must move... The key point is that space-time is not a fixed given, but rather is a heterogeneous multiplicity arising out of entities (what I now call “machines“) and signs that is constantly shifting and changing in the structure of its paths and attendant gravity. The practice of onto-cartography consists in mapping these assemblages and gravitational path so as to intervene in them and change them.
If Bryant continues to work in his current "decorative" style, I'd say that there's little to no chance that onto-cartography will itself make a substantive contribution to mapping, much less to intervention and change. The terms of the mapping and the tactics, strategies, and politics of intervention will come from other, already existing, disciplines and modes of thought. The practice of onto-cartography will consist in coining terms that can be used to attach examples to Bryant's larger theory as ornaments.
On the other hand, who knows? Perhaps when he has accumulated enough examples he'll start to think about them in a new way. One can hope.
* * * * *
Exercises for the Reader: Jargon Space
In the Warner Brother’s classic cartoon, Duck Dodgers in the 24½th Century Daffy Duck plays the role of Duck Dodgers while Porky Pig plays his unnamed sidekick. They are tasked with finding Planet X. Here’s Daffy explaining to Porky how they’ll get there:
Here’s what he’s saying:
... here is the course we shall pursue to find Planet X. Starting from where we are we go thirty-three thousand six hundred turbo miles due up. Then West in an astroarc deviation to here. Then following the great circle down seven radial lubes South by down East, by asto astrobal to here, here, and here, then by space navigal compass to here, here, and then to here and here, by thirteen stratocumulus bearing four million light years and thus to our destination.
Later in the scene Porky points out a window and suggests that, if they follow the letters in order, they’ll get to Planet X.
1) Translate Daffy’s directions into acceptable English. What’s the minimum number of words necessary for doing this?
2) Google Translate provided the following translation of Daffy’s directions into Japanese:
ここでは惑星Xは、我々は原因まで三十から三千六百ターボマイルを行くどこから始めて見つけるために追求するコースです。そして、ここにastroarc偏差西。その後、ここasto astrobalによってここに、サウスイースト·ダウン7ラジアルローションダウン大円に続いて、ここで、次に4つの万光年を冠した13層積雲でここまで、ここで、そしてこことここにスペースnavigalコンパスによるしたがって、私たちの目的地へ。
I then had Google translate the Japenese back into English, thus:
Planet X, in this case, we will pursue this course in order to find where to start to go the turbo from thirty three thousand six hundred miles up the cause. And here astroarc west deviation. Then, here, following the great circle down South East down by seven radial asto astrobal lotion here, here, to here, here and here and here, ten thousand light-years in the stratocumulus 13 bearing the next four Therefore by the space navigal compass, to our destination.
What does this tell you about the properties of jargon space? Consider the Adams Conjecture, namely: All sufficiently long strings of Google translations from one language to another will converge on 42.
3) Daffy and Porky do in fact get to Planet X. Did they get there by following Daffy’s directions or Porky’s?
4) Consider the possibility that Levi Bryant is like either Daffy or Porky. Which one? Give at least three characteristics of both which justify your answer. In particular consider the fact the one of the two actually looks at the world while the other does not.





No comments:
Post a Comment