 |
| Example 1: Overall |
This is the first in a series of posts about the art of Jamie Bérubé, who has Down syndrome. He is the son of Michael Bérubé, who has just published a book about him: Life as Jamie Knows It: An Exceptional Child Grows Up (Beacon Press, 2016). I will be reviewing the book over at 3 Quarks Daily. Michael–I can call him that, as he is a friend–wanted to include a generous selection of Jamie’s art in the book, but, as you know, color reproduction is expensive. Instead, he put it online. I took a look, became fascinated, and decided to write a series of posts about it before posting my review.
This first post is about images based on colored dots. Here’s what Michael says about these images:
I have included only 18 of his “dots” series here, mostly because he does these less often than towers, geometrics, swirls, etc. but partly because they are self-explanatory. The color of the dots is usually random, but I have included four pages on which he was very clearly experimenting with various color palettes– red, blue, yellow/green, red/orange.....
Here’s one of those images where Jamie is experimenting with various palettes:
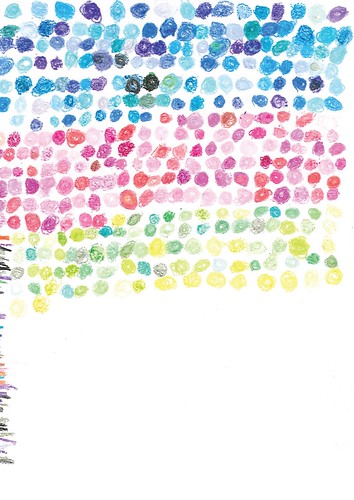 |
| Example 2: Three Palettes |
What’s going on here is obvious, almost. Notice that, for the most part, there’s variation in shades from one dot to the next on each line.
By contrast, Example 1 (above top) is one of those random ones, as is Example 3:
By contrast, Example 1 (above top) is one of those random ones, as is Example 3:
 |
| Example 3: Overall |
They’re not random, not if random means “no order whatsoever.” There’s order there, a rhythm; but it’s difficult to describe. Hence, “random.”
Let’s do a thought experiment. Remember those magical mythical monkeys that type away randomly and eventually produce Shakespeare’s Hamlet, not to mention Aunt Bessie’s recipe for omelets? The point of those monkeys is that, if their acts are truly random, then anything is possible and, in time, anything must necessarily happen. Hence Hamlet.
So, imagine an army of magical imaginary Jamies, dotting away furiously, but meticulously, on large pieces of paper, so large they can get, say, 4000 dots across. If their process is truly random, then sooner or later we’re going to see da Vinci’s Last Supper (in 4K) and a whole raft of Andy Warhol soup cans. But if the imaginary Jamies are doing what the real Jamie did then, no, we’ll never see any of those things. All we’ll see is dots, apparently at random. But not really.
Take a close look at one of those randoms. Start at the upper left, say, and scan along a row. As you move from one dot to the text, the color changes, perhaps not always (look at the right-hand side of Ex. 2, 3 and 4 from the right edge), but mostly. Look at dots in adjacent rows. Do you see same-color dots next to one another? Not often.
So, there is order here: Don’t put same color dots right next to one another. That’s a principle, a rule, and Jamie’s following it. It’s a local rule, and a simple one at that. But if you look at the overall pictures, there’s a rhythm there, some kind of spatial periodicity. Not easy to describe, but you can sense it. Jamie’s using a relatively limited set of colors. Sooner or later he’s got to repeat a color; sooner or later he’s got to repeat all of them. The local avoidance rule means he won’t repeat immediately; he’ll wait. The result is emergent global order.
It’s a bit like getting something from nothing. Jamie doesn’t have a global plan. Just a local one. But the nature of his local plan is such that global order is inevitable. Like magic. Could that be what interests him, magic?
Now let’s get curious. What’s the overall distribution of colors in an image? Does he use each color more or less the same number of times or does he favor some colors? I don’t know. You’d have to count. What about similar colors? “Not the same” is one thing if we only have black and white dots. But Jamie’s got a range of colors. Blue and turquoise are not the same, but they’re more alike than blue and red, or blue and yellow. What about the level of similarity between adjacent dots? Frankly, thinking about that one is more than I want to do.
But it’s a reasonable thing to do. Jamie was certainly thinking about it as he placed the dots, though no doubt in an intuitive non-verbal fashion. And why do you think the overall images were more interesting to him than the restricted palettes? I’m guessing it’s because keeping track of the local color configuration was more challenging (hence more interesting) and the emergence of global order more illusive (hence more interesting).
What’s going on here that the rows skew toward the upper right?
Is this a deliberate experiment? Deliberate variation in dot size and local distance? Or the result of visuo-motor fatigue of some kind?
What’s going on here? Did Jamie start drawing from the bottom (or did Michael post it upside down?)?
That dip at the upper left, inadvertent or deliberate regional variation in application of the local rule? How would you tell?
On the other hand, I’m pretty sure the sparseness of this one is deliberate:
Notice the gentle S-curve that emerges along the left. But why did I say it emerges along the left? Because I’m assuming Jamie started drawing from the right, using the right edge as a reference point. And you know what else I think? I think he drew this one in columns, rather than rows. But then why did I assume that he drew the others in rows?
Good questions all. And it doesn’t much matter whether or not I’ve been right in my various assumptions. The overall point is that there is obviously order and deliberation here, but what it is isn’t so obvious, though some things could be cleared up simply by observing Jamie at work. The thing is, though, that human behavior is complex. There’s lots to observe. What’s important and what’s merely contingent? Not so obvious.
Here’s one last image:
This is a nice overall image. The placement of dots is highly regular, though not so regular as you’d get if the paper had a grid on it (graph paper). The interesting thing is that the placement is so regular that here and there Jamie’s skipped a dot, sorta like Lucy pulling the football away just as Charlie Brown’s foot was about to connect with it. (He does the same thing in 1 and 3.)
* * * * *
Exercise No. 1: Jamie loves music, and his dad is a rock-and-roll drummer, so’s his older brother Nick, I believe. In what way are these drawings like drum beats?
Exercise No. 2: There’s an important theorem in math called the four-color theorem:
In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Two regions are called adjacent if they share a common boundary that is not a corner, where corners are the points shared by three or more regions.
How does this bear on Jamie’s local avoidance rule?

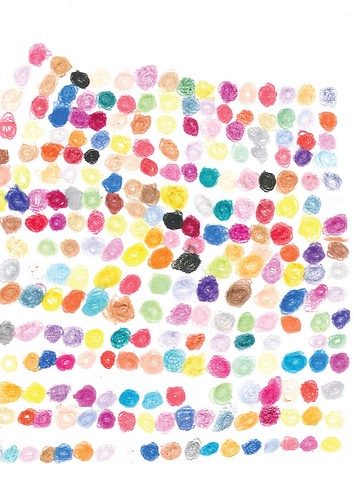

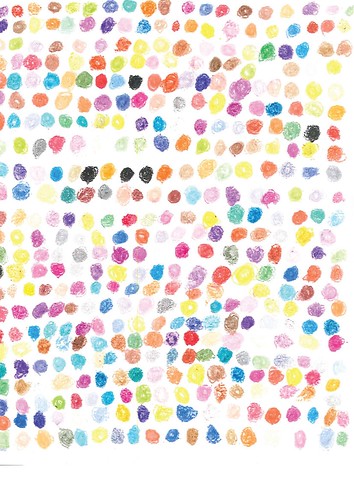
Hi Bill:
ReplyDeleteI think you'll enjoy "On the felicities of graph-based game-board design: nine" -
http://zenpundit.com/?p=52711
Nice, Charles, thanks.
ReplyDelete