Three Against Two: Splitting the Mind [augmented with new material]

I'm bumping this to the top of the queue with the addition of a tweet linking to a study of hemispheric timing (see last two sections below, Two Hemispheres, Splitting the Mind? You can download a slightly different version of the original post at THIS LINK).

* * * * *

Interesting new paper about the perennial question of lateralization and timing, from Chris Kell's lab in Frankfurt https://t.co/AeoVe5x9Zo Differential contributions of the two human cerebral hemispheres to action timing

— David Poeppel (@davidpoeppel) November 21, 2019

Abstract from the article: Anja Pflug, Florian Gompf, et al., Differential contributions of the two human cerebral hemispheres to action timing, eLife 2019;8:e48404 DOI: 10.7554/eLife.48404:

Abstract: Rhythmic actions benefit from synchronization with external events. Auditory-paced finger tapping studies indicate the two cerebral hemispheres preferentially control different rhythms. It is unclear whether left-lateralized processing of faster rhythms and right-lateralized processing of slower rhythms bases upon hemispheric timing differences that arise in the motor or sensory system or whether asymmetry results from lateralized sensorimotor interactions. We measured fMRI and MEG during symmetric finger tapping, in which fast tapping was defined as auditory-motor synchronization at 2.5 Hz. Slow tapping corresponded to tapping to every fourth auditory beat (0.625 Hz). We demonstrate that the left auditory cortex preferentially represents the relative fast rhythm in an amplitude modulation of low beta oscillations while the right auditory cortex additionally represents the internally generated slower rhythm. We show coupling of auditory-motor beta oscillations supports building a metric structure. Our findings reveal a strong contribution of sensory cortices to hemispheric specialization in action control.

* * * * *

Three against two is one of the most important rhythm ‘cells’ in all of music. What do I mean, three against two? You play three evenly spaced beats in one ‘stream’ in the same period of time you play two evenly spaced beats in another ‘stream.’ It sounds simple enough but, the problem is that three and two do not have a common divisor, making the ‘evenly spaced’ part of the formula a bit tricky. The two patterns coincide on the first beat, but the second and third beats of the three-beat stream happen at different times from the second beat of the two-beat stream. And if you think that’s a lot of verbiage for something that ought to be simple, when then you’re beginning to get the idea.

In some cultures, including many in Africa, young children are taught 3 against 2 at a very young age. For them it IS easy. That’s not the case, however, in European derived musical traditions. Three against two is not part of basic toddler pedagogy and, as a consequence, learning to do it is a bit more difficult when, and if, the time comes – for some, it never comes. Thus, within the context of the Western classical tradition, three against two is considered moderately difficult rather than being fundamental. Such rhythms are exceptional in classical music, but they are common enough that any moderately skilled keyboard player must know how to execute them.

Go Slow, Count it in Six

In playing percussion or a keyboard instrument it is easy to alternate notes from one hand to the other and it is easy to play notes simultaneously with both hands. It is also easy to play two or four or eight notes with one hand against one note with the other hand or, for that matter, three or six notes with one hand against one note with the other. And, of course, it is easy to repeat such figures time after time after time. It is, however, distinctly more difficult to play three notes with one hand against two with the other. The problem is that, once the first note is struck by both hands, none of the successive notes in the pattern line up nor are they equidistant from one another. The patterns are incommensurate, as we see in the following diagram:

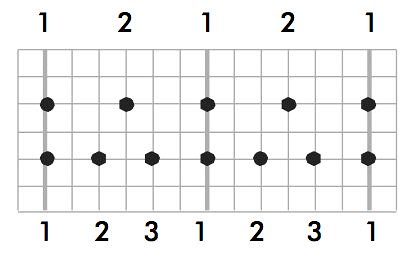Three Against Two

Let’s consider the advice Joseph Hoffman offered on this problem. Hoffman was a piano virtuoso whose career spanned the late nineteenth and early twentieth centuries. In 1909 he published a book of Piano Questions, which consisted of “direct answers to two hundred fifty questions asked by piano students” which he had originally published in the Ladies’ Home Journal over a period of two years. One of the questions he answered was “How must I execute triplets played against two-eighths?” — a typical 2-against-3 pattern. Here is the first part of Hoffman’s answer:

In a slow tempo it may serve you to think of the second eighth-note of the triplet as being subdivided into two sixteenths. After both hands have played the first note of their respective groups simultaneously, the place of the aforsaid sixteenth note is to be filled by the second note of the couplet.

Hoffman is, in effect, urging the student to count the passage in six, where each beat is a sixteenth note. We can diagram this strategy as follows:

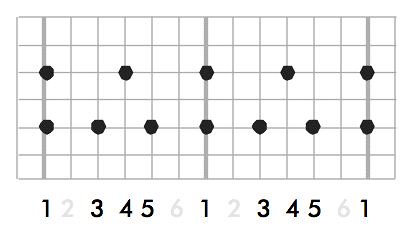Counting in Six

The (appropriate finger in the) hand executing the duplet (2) patterns strikes a note on beats one and four of the cycle while the (appropriate finger in the) hand executing the triplet (3) patterns strikes a note on beats one, three, and five of the cycle. No notes are struck on beats two and six and both hands strike a note on beat one. Counting in this way one can execute the triplet notes with the one hand and the duplet notes with the other.

When Going Fast, Just Do It

After explaining how to handle three against two (3/2) in a slow tempo Hoffman goes on to explain what to do at a faster tempo. His advice here is quite different:

In faster motion it is far better to practise at first each hand alone and with somewhat exaggerated accents of each group until the two relative speeds are well established in the mind. Then try to play the two hands together in a sort of semi-automatic way. Frequent correct repetition of the same figure will soon change your semi-automatic state into a a conscious one, and thus train your ear to listen to and control two different rhythms or groupings at the same time.

The question that arises is: Why this rather different advice? Sure, things change when you go faster, but why? In particular, why doesn’t he tell the student simply to start by learning the passage at a slow tempo and then gradually speed it up?

Two Hemispheres

We do not have answers to these questions. One obvious suggestion follows from a fact and a possibility. That fact is that the left hemisphere of the brain controls the right side of the body while the right hemisphere controls the left side of the body. This crossover is beside the argument I want to make. All that’s important is that the each side of the body is controlled by a different hemisphere.

The possibility is that music’s basic timing is regulated in the left hemisphere. That means timing information is directly available to the right side of the body. There will, however, be a small time-lag for the left side of the body as the timing information has to cross from one side of the brain to the other.

Here then, is my suggestion: When the 3/2 pattern is slow enough there is no difficulty timing both hands from one hemisphere despite the fact that the timing loop for the right-hemisphere (controlling the left hand) must go through the corpus callosum whereas the left-hemisphere loop is entirely within that hemisphere. But once the tempo goes beyond a certain point — which has not, to my knowledge, been measured – the inter-hemispheric lag might become a problem, making it difficult for the left hand (controlled by the right hemisphere) to get timing pulses quickly enough.

At this point the motor system would have to shift into a different mode, or phase, of operation. What might this other mode be? The obvious suggestion is that we shift from timing both hands from one hemisphere — the dominant one (the left hemisphere for most people) — to a mode where each hand is timed by its own hemisphere, thus eliminating the lag inherent in communicating from one hemisphere to the other.

Splitting the Mind?

Notice that Hoffman used the term “semi-automatic.” You have to give up some control; too much effort at control will mess you up by attracting the non-dominant rhythm to the dominant one. Once that happens, the left hemisphere can generate its own timing loop independently of the right. [And there is, in fact, some suggestive empirical evidence suggesting that, in complex bimanual tapping tasks, each hand has its own timer. 

This is an important point, and leads to another issue: If we have two independent timers, one in each hemisphere, what controls the interaction between these them so they keep time together? The question, of course, is a loaded one as it assumes that we need something to control that interaction. It would be more parsimonious to imagine that the two timers, the right and the left, are simply coupled together through the corpus callosum without there being any explicit high-level regulation of their interaction. The two timers “negotiate” their mutual timing directly with one another; the interaction is self-organizing.

In this context it is thus interesting to note that musicians, especially those who started their training at a young age, are known to have a larger corpus callosum than most people. This would, of course, facilitate interaction between the two hemispheres. Such interaction would be helpful for playing instruments that require significant involvement of both hands, that is to say, most instruments except brass instruments. Such interaction, of course, could involve both one hemisphere directing activity in the other hemisphere and the kind of mutual entrainment required of up-tempo three-against-two patterns.

I will leave it as an exercise for the reader to ponder whether or not such ‘splitting of the mind’ has any philosophical implications for thinking about The Self. If neither hemisphere is subordinate to the other, if there is no SINGLE ULTIMATE NEURAL COMMAND CENTER, then who’s in charge?

Anyone?

No one?

Dos the question involve a category mistake?