Some notes on computers, AI, the mind, and the sorry@$$ st8 of general understanding on these matters, that’s the title of my current piece at 3 Quarks Daily (minus the crossed out part). I’d wanted to include something more substantive on the difference between machine translation back in the era of so-called symbolic computing and the current technology and current technology, which is based on a varieyt of statistically based machine learning technology. But it was clear that I just couldn’t squeeze it in. Plus, I’m still thinking about that one. But here’s a first go.
About a decade ago the Association for Computational Linguistics presented Martin Kay with a Lifetime Achievement Award. He had been a first generation researcher in machine translation and remains academically active. In the address he makes upon acceptance of the award he offered a number of observations about the difference between symbolic language processing and statistical processing. This is the last of four such remarks (pp. 12-13):
This, I take it, is where statistics really come into their own. Symbolic language processing is highly nondeterministic and often delivers large numbers of alternative results because it has no means of resolving the ambiguities that characterize ordinary language. This is for the clear and obvious reason that the resolution of ambiguities is not a linguistic matter. After a responsible job has been done of linguistic analysis, what remain are questions about the world. They are questions of what would be a reasonable thing to say under the given circumstances, what it would be reasonable to believe, suspect, fear or desire in the given situation. If these questions are in the purview of any academic discipline, it is presumably artificial intelligence. But artificial intelligence has a lot on its plate and to attempt to fill the void that it leaves open, in whatever way comes to hand, is entirely reasonable and proper. But it is important to understand what we are doing when we do this and to calibrate our expectations accordingly. What we are doing is to allow statistics over words that occur very close to one another in a string to stand in for the world construed widely, so as to include myths, and beliefs, and cultures, and truths and lies and so forth. As a stop-gap for the time being, this may be as good as we can do, but we should clearly have only the most limited expectations of it because, for the purpose it is intended to serve, it is clearly pathetically inadequate. The statistics are standing in for a vast number of things for which we have no computer model. They are therefore what I call an “ignorance model”.
That last point is very important: “...to stand in for the world construed widely...” YES! Back in the old days we – though I never worked on machine translation I include myself because I did work on computational semantics – certainly gave serious thought to creating computer models of semantics, broadly construed to cover common sense knowledge, myths and stories, and even scientific theories. We didn’t get very far, but, yes, we attempted to take the measure of the problem.
That’s what’s been abandoned.
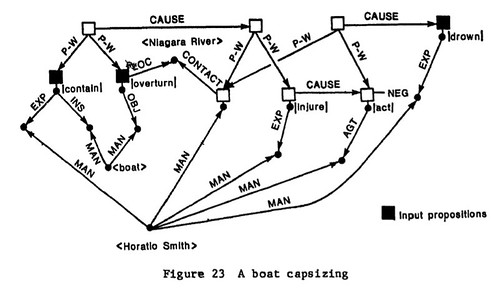
Let me offer a small example of computational semantics. This is from a model Brian Phillips had devised for recognizing tragic stories about drowning men:
The nodes (junctures) represent various kinds of entities (things, properties, events, what have you) while the arcs (lines, links) between them represent relationships between those entities. Notice the labels all over the place. They identify the relationships and the entities. The actual geometrical arrangement of those visual objects is of little consequence, except to the extent that it affects how us humans read the diagram. Where the specific nodes are is irrelevant. All that matters is what is connected to what and the labels on everything. There is a logic governing those relationships and entities, a logic expressed in terms of inferences guided by those labels. That logic is all that matters.
Where did that semantic structure come from? Phillips made it up. No, not out of thin air. There is justification in the psychological and linguistic literature for some aspects of the structure. And Phillips worked in the context of a research group, of which I was a member, convened by David Hays, another first generation researcher in machine translation (and who had hired Martin Kay to work with him at RAND back in the 1950s). That network represents what was then our best sense of a (very very small fragment) of the world knowledge Kay refers to.
How, then, could one do machine translation, and fairly effective translation at that (at least for limited purposes), without such world knowledge, without semantics, and hence without understanding? Good question. I’ll give you a clue.
It comes from a useful piece by Jay Alammar:
By design, a RNN [recurrent neural network] takes two inputs at each time step: an input (in the case of the encoder, one word from the input sentence), and a hidden state. The word, however, needs to be represented by a vector. To transform a word into a vector, we turn to the class of methods called “word embedding” algorithms. These turn words into vector spaces that capture a lot of the meaning/semantic information of the words (e.g. king - man + woman = queen). [2]
That’s the crucial point, each word is represented by a vector. What is that? you ask. Good question. To answer that we need to explain a bit distributional semantics – the statistics that Martin Kay mentions. I’m not going to attempt that here, and really, I’m not the one to do it, but I’ve taken a crack at it in the past [3].
But I can make an observation about that example, king - man + woman = queen. It is easy enough for us to parse it and see what’s going on:
A king is a male monarch. We take the idea of king and subtract from it the idea of man, leaving the idea of monarch. When we add the idea of monarch to the idea of woman we get the idea of queen. A queen is a female monarch.
What does that have to do with vectors? A vector is a mathematical object that is both numerical and geometric. Think of it as a bunch of numbers that characterize a point in space. What’s going on in this kind of statistical semantics is that, using a procedure that’s fairly straightforward though computationally intense, each word is located at a point in a high-dimensional space. A word’s vector is simply an ordered list of numbers, each of which specifies its location on one of the dimensions of that space.
What that expression is doing is moving from one position in that high dimensional space, the position for king, to another position, the one for queen. How does it get there? By subtracting the values (vector) for man and then adding the resulting set of values to those (vector) for woman. It’s all about numbers that specific positions in space.
Prior to any attempt at translation each word in a language has been associated with a vector that assigns it a position in this high dimensional space. To a first approximation that high dimensional space is pretty much the same for all languages. Why? Because the world is pretty much the same – pretty much, but certainly not entirely so. Cats, dogs, oranges, apples, rivers, mountains, the sun, moon, people, flags, glasses, and so on and so forth, all of these are pretty much the same and stand in pretty much the same relationships with one another.
To translate from one language to another, then, we must, 1) associate the vectors for the words in the source language with the matching vectors for the target language and then, 2) get the target language morphology and syntax right. Neither or those is a trivial job, but they’re not rocket science. The rocket science is in getting those high dimensional vector spaces set up in the first place. But that’s all it is, rocket science, very sophisticated rocket science. It’s not magic, it’s not voodoo. And it doesn’t answer Martin Kay’s pleas for semantic knowledge. Sophisticated though it is, it remains, as he says, an ignorance model [4].
Now, let’s compare these two systems. In the symbolic computation semantics we have a relational graph where both the nodes and the arcs are labeled. All that matters is the topology of the graph, that is, the connectivity of the nodes and arcs, and the labels on the nodes and arcs. The nature of those labels is very important.
In the statistical system words are in fixed geometric positions in a high-dimensional space; exact positions, that is, distances, are critical. This system, however, doesn’t need node and arc labels. The vectors do all the work.
I could, and should, say more. But this is enough for now. I will note that we can get rid of both the node and arc labels in the symbolic system, but to do so we have to connect it to the world, something David Hays wrote about, Cognitive Structures, HRAF Press, 1981.
More later.
[1] Martin Kay, A Life of Language. Computational Linguistics 31 (4), 425-438 (2005): http://web.stanford.edu/~mjkay/LifeOfLanguage.pdf.
[2] Jay Alammar, Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention), May 25, 2018: https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/.
[3] I’ve said a bit about this in a post from last year, Notes toward a theory of the corpus, Part 2: Mind, December 3, 2018: https://new-savanna.blogspot.com/2018/12/notes-toward-theory-of-corpus-part-2.html.
[4] And it is prone to some very peculiar failures. See the posts at Language Log under the label, “Elephant semific”: https://languagelog.ldc.upenn.edu/nll/?cat=299.
One final note: For what it is worth, this post begins to satisfy the itch I've been scratching in several posts, perhaps most centrally, Borges redux: Computing Babel – Is that what’s going on with these abstract spaces of high dimensionality?




No comments:
Post a Comment